Understanding Push Sum and Gossip Protocols
October 24, 2020 • 5 min read • Code
Last week I worked with Gossip algorithms as a part of the Distributed Operating System class under Prof. Alin Dobra. Distributed Systems have always been an interesting topic and once you read it's a rabbit hole down from there.
As the scale of distributed systems increases, there is a massive instability in the network because of numerous nodes. Gossip protocols work similarly to the covid-19 epidemic situation we are living in right now. As the name suggests, these protocols work similarly to the spread of the virus to effectively communicate information between nodes. Sometimes these Gossip algorithms are also known as Epidemic algorithm because of their behavior. The goal of this project was to determine the convergence of such algorithms through a simulator based on actors written in F# on various network topologies.
Topologies
The actual network topology plays a critical role in the dissemination speed of Gossip protocols. As part of this project, I've experimented with various topologies. The topology determines who is considered a neighbor in the above algorithms.
Full Network: Every actor is a neighbor of all other actors. That is, every actor can talk directly to any other actor.
2D Grid: Actors form a 2D grid. The actors can only talk to the grid neighbors.
Line: Actors are arranged in a line. Each actor has only 2 neighbors (one left and one right, unless you are the first or last actor).
Imperfect 2D Grid: Grid arrangement but one random other neighbor is selected from the list of all actors (4+1 neighbors).
Gossip
_10ProcessInformation ->_10 if rumourCount < 11 then_10 let rnd = Random().Next(0, neighbours.Length)_10 if not converged_nodes.[neighbours.[rnd]] then_10 neighbours.[rnd] <! CallWorker_10 mailbox.Self <! ProcessInformation
The node (A) in the network randomly selects another node to share information. Here, it is assumed that each node in the network maintains a list of all other nodes, or obtains information from a centralized server (in the code snippet, "neighbors" are lists that maintains list of neighboring nodes).
On receipt of information, the receiving node (B) processes the information. The above snippet is a straightforward implementation of actor that accepts a message and sends a message to random neighbor
_10CallWorker ->_10 if rumourCount = 0 then _10 mailbox.Self <! ActivateWorker_10 if (rumourCount = 10) then _10 supervisor <! ReportMsgRecvd "Rumor"_10 converged_nodes.[mailbox.Self] <- true_10 rumourCount <- rumourCount + 1
In the next round of this process, both A and B again select nodes randomly and transmit the information
Each actor keeps track of rumors and how many times it has heard the rumor. It stops transmitting once it has heard the rumor 10 times (10 is arbitrary, you can select other values)
The entire network is said to be converge once all the nodes have received information for at least 10 times.
Result
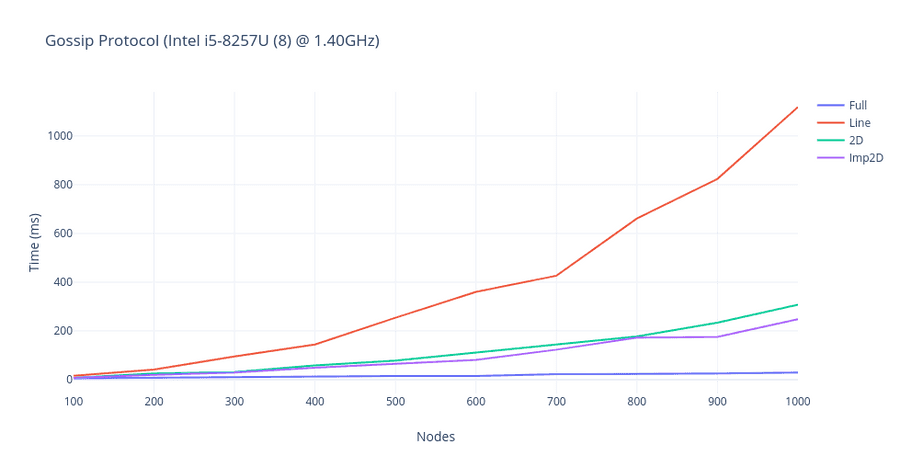
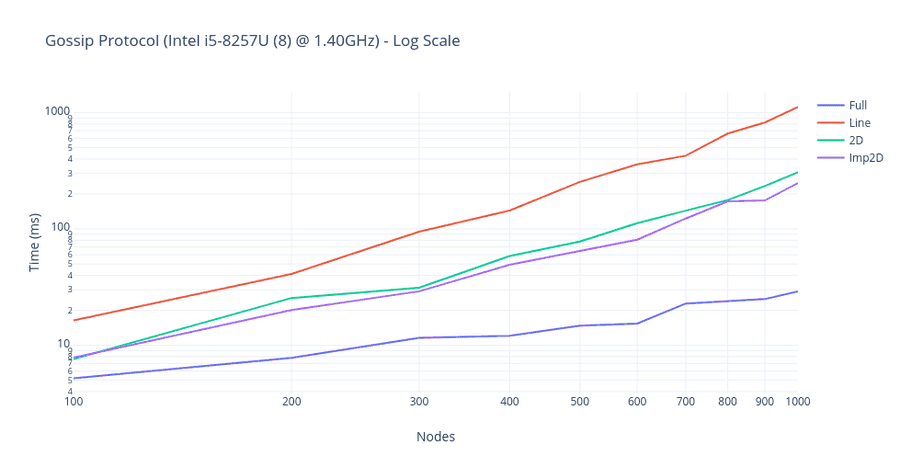
-
Line topology is the slowest to converge. This is because it has only access to 2 neighbors (left and right node).
-
Full topology is the fastest to converge in all scenarios. This is because they connect it to all the nodes and convergence is faster to achieve in this scenario.
-
As expected, 2D and imperfect 2D would achieve the convergence time in between the line and full with imperfect 2D performing slightly better or equal to 2D performance.
PushSum
_10StartPushSum delta ->_10 let index = Random().Next(0, neighbours.Length)_10_10 sum <- sum / 2.0_10 weight <- weight / 2.0_10 neighbours.[index] <! ComputePushSum(sum, weight, delta)
The push sum protocol is one of the gossip-based aggregation algorithms that is based on the interactive pairwise distribution of aggregated values among particulars entities.
_25ComputePushSum (s: float, w, delta) ->_25 let newsum = sum + s_25 let newweight = weight + w_25_25 let cal = sum / weight - newsum / newweight |> abs_25_25 if alreadyConverged then_25_25 let index = Random().Next(0, neighbours.Length)_25 neighbours.[index] <! ComputePushSum(s, w, delta)_25 else_25 if cal > delta then_25 termRound <- 0_25 else _25 termRound <- termRound + 1_25_25 if termRound = 3 then_25 termRound <- 0_25 alreadyConverged <- true_25 supervisor <! Result(sum, weight)_25 _25 sum <- newsum / 2.0_25 weight <- newweight / 2.0_25 let index = Random().Next(0, neighbours.Length)_25 neighbours.[index] <! ComputePushSum(sum, weight, delta)
To properly fulfill the mentioned functionality, the entities store two values: the value of the averaged quantity and the weight. The entities are assigned an initial value, which is updated at each iteration in terms of the information from the adjacent nodes and the inner state. The parameter weight is set to 1 for each entity at the beginning of the whole process
It sends this entity the half of the value of its average quantity and the half of its weight. After all, complete this procedure, each entity calculates the average estimation by counting the ratio of the sums of these two parameters
Result
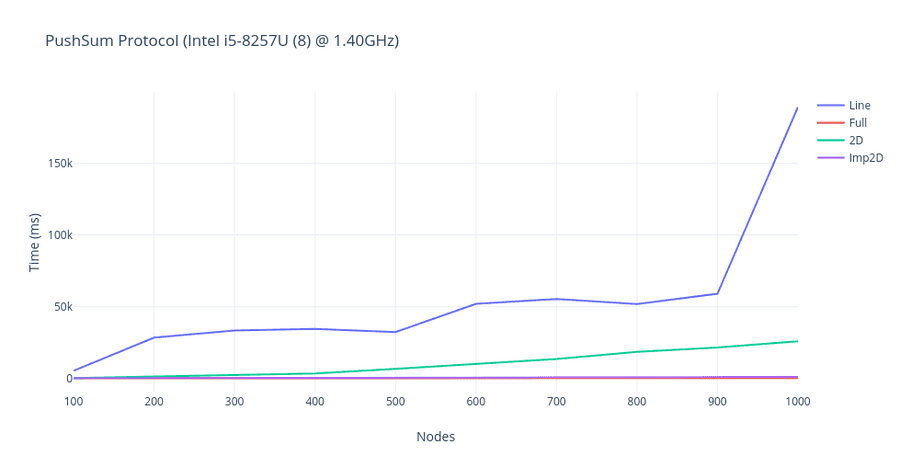
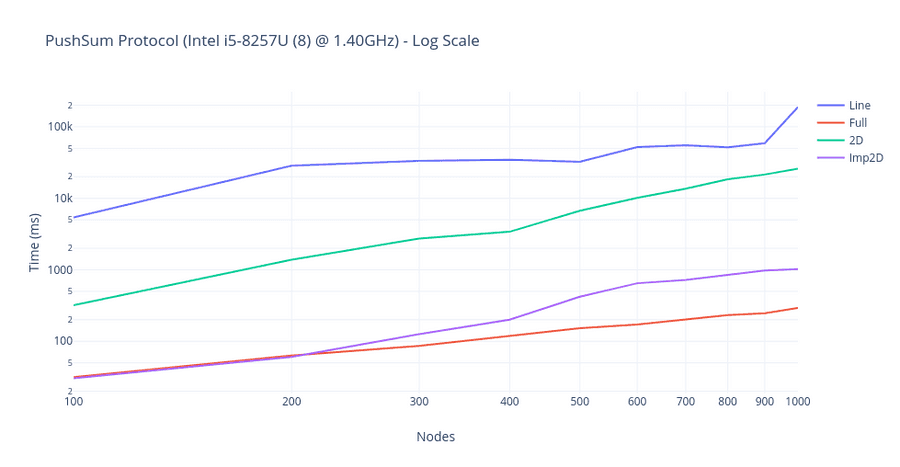
If you want to get started with some of these algorithms, I would highly recommend reading Epidemic algorithms for replicated database maintenance and Gossip-Based Computation of Aggregate Information
← Guide to Hacktoberfest and winning a free T-ShirtConfigure Nginx Proxy Manager with Bitwarden →